- Worksheets>
- Math>
- How to Solve>
- Absolute Value Inequalities
Follow the systematic procedure to solve absolute value inequalities. Different examples provided in each step for better understanding of procedures involved. (Take me directly to solved examples)
Step 1: Standard Form
Arrange the inequalities such that the absolute value expression stays to the left and the coefficient always 1.
For example, 2 | 3x + 5 | + 4 < 8
Subtract 4 on both sides
2 | 3x + 5 | + 4 - 4 < 8 - 4
2 | 3x + 5| < 4
Divide by 2 on both sides,
![]()
| 3x + 5 | < 2
Now the coefficient of absolute value expression becomes 1. ( |3x + 5| is as same as 1 |3x + 5| )
Let us see the example with negative coefficients.
-2 | 3x + 5 | < 4
Dividing by -2 on both sides,
| 3x + 5 | > -2 (inequality reversed)
Important note: When you multiply or divide wtih negative numbers, inequality reversed.
Step 2: Check the Existence of Solutions
Consider the example |5x + 2| < -3
Look at the inequality and the constant term in right hand side.
![]()
| 5x + 2 | < -3
Absolute value of 5x + 2 is positive. However, inequality is less than -3 (negative number), which is not possible. Positive number is always greater than the negative number. The solutions of such absolute value inequalities are extraneous. In simple, no solution exists for this particular type of absolute value inequality.
Step 3: Split into Algebraic Inequalities
If the solution exists, rewrite absolute value inequality into two different algebraic inequalities.
For example, 3 |2x + 3| < 15
After applying step 1 and step 2, we have |2x + 3| < 5 (solution exists).
Splitting that into two different inequalities, we have
2x + 3 < 5 ... (i)
- (2x+3) <5 ... (ii)
How do we write the absolute value inequality |x + 5| > 6 into two different algebraic inequalities?
In order to frame the first inequality, remove the vertical bars and take the expression alone. So, we have
x + 5 > 6 ...(i)
To frame the second inequality, remove vertical bars and take minus of the entire expression between the bars.
So, we have - ( x + 5 ) > 6 ...(ii)
Step 4: Solve the Algebraic Inequalities
Now, as a final step, solve the algebraic inequalities to find the solution.
For example, |2x + 3| < 5
Applying step 3, we have
2x + 3 < 5 ... (i)
- (2x + 3) < 5 ... (ii)
Inequality 1:
2x + 3 < 5
Subtract 3 on both sides
2x < 2
Divide by 2 on both sides
x < 1 ... (Solution 1)
Inequality 2:
- (2x + 3) < 5
Distribute -1
-2x - 3 < 5
Add 3 on both sides
-2x < 8
Divide by -2 on both sides
x > -4 (Inequality reversed because of division of -2) ... (Solution 2)
Step 5: Write the Solution Set
We may write solution in four different ways.
1) Standard notation
2) Graph representation
3) Interval notation
4) Set builder form
Table below shows how the solution will be written in different forms. First column is a list of inequalities in standard form.

For the example provided in step 4, the answer in
Standard form: x > -4 and x < 1 (or) -4 < x < 1
![]()
Interval notation: (-4, 1)
Set builder form: {x | -4 < x < 1, x is real}
Look at the examples below to understand how much easy is solving absolute value inequalities.
Solved Example 1:Check for the existence of solutions:
![]()
Solution:
![]()
a) and b) have solution. Removal of negative sign for c) and d) by multiplying -1 will reverse the inequality and change the sign of the constant as well. For c), | x | < -6, and the solution is not possible. For d) inequality reversed to 'greater than or equal' symbol.
All of the above except c) contain solutions.
Solved Example 2:Solve the absolute value inequalities:
![]()
Solution:
![]()
Step 1: It is in standard form.
Step 2: Inequality is "less than" symbol and the constant term at right hand side is negative. No solution exists.
![]()
Step 1: It is in standard form.
Step 2: Inequality is "greater than" symbol. Solution Exists.
Step 3: Split into algebraic inequalities.
x - 1 > 2 ... (i)
-(x - 1) > 2 ... (ii)
Step 4: Solve
x - 1 > 2 ... (i)
x > 3
- (x - 1) > 2 ... (ii)
-x + 1 > 2
-x > 1
x < 1
Step 5: Final solution
In general form, x < 1 or x > 3
![]()
Interval notation:
![]()
In set builder form,
![]()
![]()
Step 1: Set the inequality in standard form.
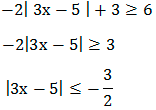
Step 2: Inequality is "less than equal" symbol and the constant term at right hand side is negative. No solution exists.
![]()
Step 1: Bring it to the standard form.
3 | 2x + 1 | < 15
| 2x + 1 | < 5
Step 2: Solution exists.
Step 3: Set up algebraic inequalities
2x + 1 < 5 ... (i)
- (2x + 1) < 5 ... (ii)
Step 4: Solve
2x + 1 < 5
2x < 4
x < 2
- (2x + 1) < 5
-2x - 1 < 5
-2x < 6
x > -3
Step 5: Final solution
Standard form: x >-3 and x < 2
![]()
Interval notation: (-3, 2)
Set builder form: {x | x > -3 and x < 2, x is real}
Try Yourself: Absolute Value Worksheets
