- Worksheets>
- Math>
- Geometry>
- Triangle>
- Medians and Centroids
Median and Centroid of a Triangle Worksheets
Gain immense practice with this unit of printable high school worksheets on median and centroid of triangles featuring adequate skills like finding the side length with the measures presented as whole numbers and algebraic expressions, learn to find the centroid, determine the equation of the medians, the coordinates of the vertex, the indicated length and more. Access some of these worksheets for free!
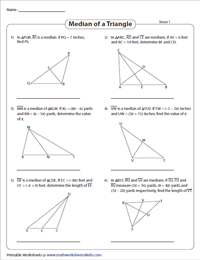
Find the Indicated Length of a Triangle containing Median
The triangles comprise one or two medians with measures offered as whole numbers and algebraic expressions. Solve for x and determine the indicated side length(s).
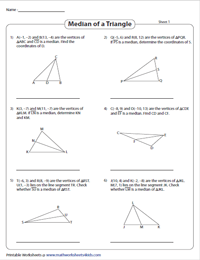
Problems involving Median, Midpoint and Distance Formula
Figure out the coordinates of the midpoint using the midpoint formula. Using the distance formula, determine the specified length, and also check if the given coordinates is the midpoint.
Find the Equations of the Medians
Determine the coordinates of the midpoint in these pdf worksheets. Use the point-slope formula or two-point formula to find the equation of the indicated median. Convert the equation to the standard form as well.
Coordinates of the Centroid using Equations of the Medians
The medians in this compilation of high school worksheets are represented as equations. Solve the systems of linear equations and find the coordinates of the centroid to complete the printable handouts.
Find the Centroid | Coordinates and Graph
Compute the centroid of the triangles by finding the average of the x-coordinates and the y-coordinates in Part A and Part C. Determine the coordinates of the triangle represented on a graph and figure out the centroid in Part B.
Set up an equation using the coordinates of the vertices and the centroid to find the third vertex in Part A. Find the missing coordinates of the vertex or centroid in Part B.
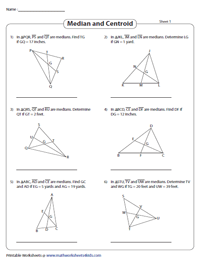
Median and Centroid | Proportions
Determine the length of the line segment from centroid to midpoint, centroid to vertex or the length of the median using the property that states - the centroid divides the median in the ratio 2:1.
Median and Centroid | Proportions involving Algebraic Expressions
Form an equation with the measures of the segments offered as algebraic expressions using the property of centroid, solve for x and find the indicated length(s).
Related Worksheets