- Worksheets>
- Math>
- Geometry>
- Triangle>
- Congruence
Congruent Triangles Worksheets
The origin of the word congruent is from the Latin word "congruere" meaning "correspond with" or "in harmony". A collection of congruent triangles worksheets on key concepts like congruent parts of congruent triangles, congruence statement, identifying the postulates, congruence in right triangles and a lot more is featured here for the exclusive use of 8th grade and high school students. A prior knowledge of triangle congruence postulates( SSS, SAS, ASA, AAS, and HL) is a prerequisite to work with the problems in this set of printable PDF worksheets. Tap into some of these worksheets for free!
Implement this collection of pdf worksheets to introduce congruence of triangles. Complete the congruence statement by writing down the corresponding side or the corresponding angle of the triangle. Answer key is included.
Write the Congruence Statement
Write congruence statement for each pair of triangles in this set of congruent triangles worksheets. Observe the congruent parts keenly and write the statement in the correct order.
Indicate the Congruent Angles and Sides
Students of grade 8 are required to mark the corresponding congruent angles and congruent sides on each pair of triangles for the given congruence statements featured in the pdf worksheets.
Identify and Write the Postulates
This range of printable worksheets is based on the four postulates AAS, ASA, SAS and SSS. Analyze each pair of triangles and state the postulate to prove the triangles are congruent.
Write the Missing Congruence Property
Observe the corresponding parts of each pair of triangles and write the third congruence property that is required to prove the given congruence postulate.
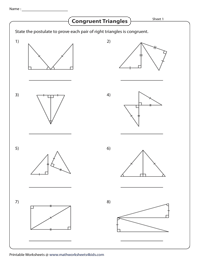
Congruence Postulates in Right Triangles
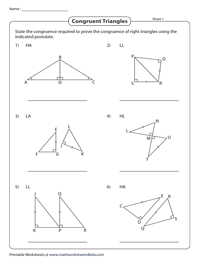
We broadly classify congruence postulates in right triangles into four: LL, HL, HA, LA. State the correct postulate to prove that each pair of right triangles in this printable practice set is congruent.
Missing Congruence Property in Right Triangles
This compilation of high school pdf worksheets focuses on the congruence of right triangles. Determine the missing congruence property in a pair of triangles to substantiate the postulate.
Related Worksheets